Solicitamos su permiso para obtener datos estadísticos de su navegación en esta web, en cumplimiento del Real Decreto-ley 13/2012. Si continúa navegando consideramos que acepta el uso de cookies. OK | Más información
Compartir en WhatsApp, sólo para móviles.

VIGAS DOBLEMENTE APOYADAS

RESUMEN DE CASOS

Pulsa en el diagrama para ir al caso elegido:

CASO 1

Diagrama forma y cargas caso 1

Definición

Viga apoyada-apoyada con una carga puntual no centrada.

REACCIONES

\[ \mathrm{R_A}=\frac{P \cdot b}{L} \]
\[ \mathrm{R_B}=\frac{P \cdot a}{L} \]
Diagrama de cargas y reacciones caso 1

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{P \cdot b}{L} \]
\[ \mathrm{V_{CB}}=-\frac{P \cdot a}{L} \]
Diagrama de Cortantes caso 1

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{P \cdot b}{L} \cdot x \]
\[ \mathrm{M_{CB}}=-\frac{P \cdot a}{L} \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\mathrm{M_C}=\frac{P \cdot a \cdot b}{L} \hspace{2em} para \hspace{1em} \mathrm{x_o}=a \]
Diagrama de momentos caso 1

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot L \cdot b \cdot x}{6 \cdot E \cdot I} \cdot (1- \frac{b^2}{L^2}-\frac{x^2}{L^2}) \]
\[ \mathrm{Y_{AC}}=\frac{P \cdot L \cdot a \cdot (L-x)}{6 \cdot E \cdot I} \cdot (1- \frac{a^2}{L^2}-\left(\frac{L-x}{L}\right)^2) \]
\[ \mathrm{Y_{AC}}=\frac{P \cdot L \cdot a \cdot (L-x)}{6 \cdot E \cdot I} \cdot (1- \frac{a^2}{L^2}-\left(\frac{L-x}{L}\right)^2) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{P \cdot b}{9 \cdot E \cdot I\cdot \sqrt{3}} \cdot (L^2-b^2)^{3/2} \]

para:

\[ x= \sqrt{\frac{(L^2-b^2)}{3}}\]
Flecha caso 1

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{P \cdot a \cdot b}{6 \cdot E \cdot I \cdot L} \cdot (L+b) \]
\[ \mathrm{\theta_C}=\frac{P \cdot a \cdot b}{3 \cdot E \cdot I \cdot L} \cdot (b-a) \]
\[ \mathrm{\theta_B}=\frac{P \cdot a \cdot b}{6 \cdot E \cdot I \cdot L} \cdot (L+a) \]


CASO 2

Diagrama forma y cargas caso 2

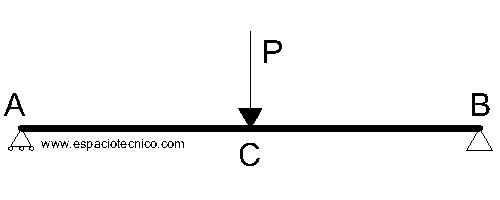
Definición

Viga apoyada-apoyada con una carga puntual centrada.

REACCIONES

\[ \mathrm{R_A}=\mathrm{R_B}=\frac P2 \]
Diagrama de cargas y reacciones caso 2

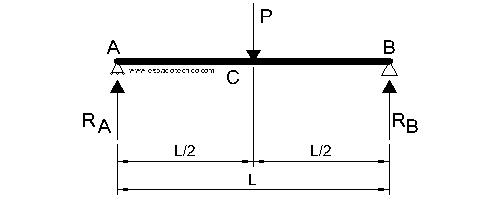
E. CORTANTES

\[ \mathrm{V_{AC}}=-\mathrm{V_{BC}}=\frac P2 \]
Diagrama de Cortantes caso 2

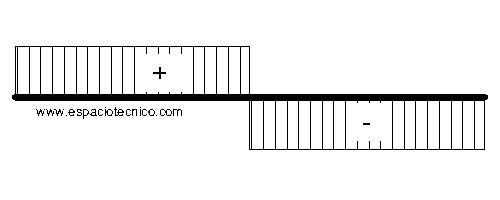
M. FLECTORES

\[ \mathrm{M_{AC}}=\frac P2 \cdot x \]
\[ \mathrm{M_{CB}}=-\frac P2 \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\mathrm{M_C}=\frac{P \cdot L}{4} \hspace{2em} para \hspace{1em} \mathrm{x_o}=\frac P2 \]
Diagrama de momentos caso 2

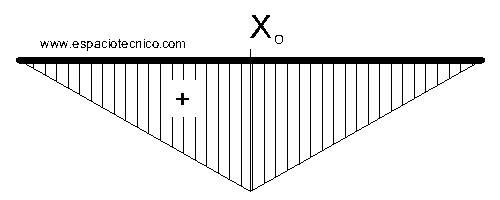
EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot L^2 \cdot x}{16 \cdot E \cdot I} \cdot (1- \frac{4 \cdot x^2}{3 \cdot L^2}) \]

FLECHA

\[ \mathrm{Y_C}=\frac{P \cdot L^3}{48 \cdot E \cdot I} \]
Flecha caso 2

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\mathrm{\theta_B}=\frac{P \cdot L^2}{16 \cdot E \cdot I} \]
\[ \mathrm{\theta_C}=0 \]


CASO 3

Diagrama forma y cargas caso 3

Definición

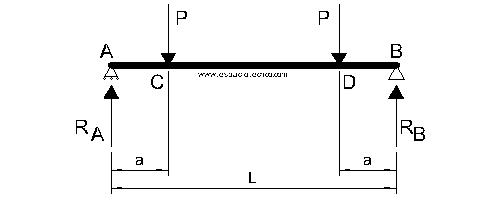
Viga apoyada-apoyada con dos carga puntuales iguales y simétricas.

REACCIONES

\[ \mathrm{R_A}=\mathrm{R_B}=P \]
Diagrama de cargas y reacciones caso 3

E. CORTANTES

\[ \mathrm{V_{AC}}=P \]
\[ \mathrm{V_{CD}}=0 \]
\[ \mathrm{V_{DB}}=-P \]
Diagrama de Cortantes caso 3

M. FLECTORES

\[ \mathrm{M_{AC}}=P \cdot x \]
\[ \mathrm{M_{CD}}=P \cdot a \]
\[ \mathrm{M_{DB}}=P \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\mathrm{M_{CD}} \]
Diagrama de momentos caso 3

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot x}{6 \cdot E \cdot I} \cdot (3 \cdot a \cdot L- 3 \cdot a^2 - x^2) \]
\[ \mathrm{Y_{CD}}=\frac{P \cdot a}{6 \cdot E \cdot I} \cdot (3 \cdot L \cdot x- 3 \cdot x^2 - a^2) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{P \cdot a}{24 \cdot E \cdot I} \cdot (3 \cdot L^2-4 \cdot a^2) \]

para:

\[ x= \frac L2 \]
Flecha caso 3

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\mathrm{\theta_B}=\frac{P \cdot a \cdot (L-a)}{2 \cdot E \cdot I} \]
\[ \mathrm{\theta_C}=-\mathrm{\theta_D}=\frac{P \cdot a \cdot (L-2 \cdot a)}{2 \cdot E \cdot I} \]


CASO 4

Diagrama forma y cargas caso 4

Definición

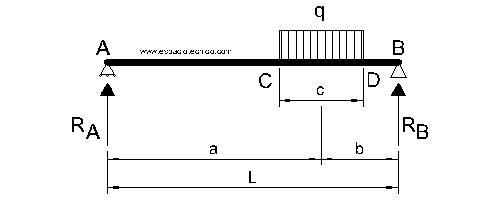
Viga apoyada-apoyada con una carga repartida aislada que no empieza ni termina en los apoyos.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot b \cdot c}{L} \]
\[ \mathrm{R_B}= \frac{q \cdot a \cdot c}{L} \]
Diagrama de cargas y reacciones caso 4

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{q \cdot b \cdot c}{L} \]
\[ \mathrm{V_{CD}}=\frac{q \cdot b \cdot c}{L}-q \cdot (\frac c2 -a+x) \]
\[ \mathrm{V_{DB}}=-\frac{q \cdot a \cdot c}{L} \]
Diagrama de Cortantes caso 4

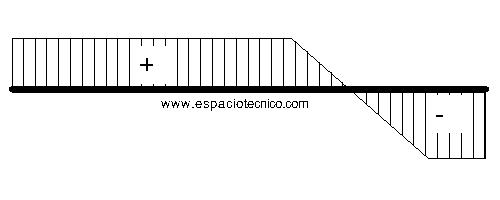
M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{q \cdot b \cdot c}{L} \cdot x \]
\[ \mathrm{M_{CD}}=\frac{q \cdot b \cdot c}{L} \cdot x - \frac q2 \cdot (x-(a-\frac c2))^2 \]
\[ \mathrm{M_{DB}}=\frac{q \cdot a \cdot c}{L} \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\frac{q \cdot b \cdot c}{2 \cdot L} \cdot (2 \cdot a-c+ \frac{b \cdot c}{L}) \]

para:

\[ \mathrm{x_{o}}= a- \frac c2+ \frac{b \cdot c}{L} \]
Diagrama de momentos caso 4

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot b \cdot c}{6 \cdot L} \cdot \frac{x}{E \cdot I} \cdot (-x^2+a \cdot (L+b- \frac{c^2}{4 \cdot a})) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot b \cdot c}{6 \cdot L} \cdot \frac{x}{E \cdot I} \cdot (-x^2+a \cdot (L+b- \frac{c^2}{4 \cdot a})) \]
\[ \mathrm{Y_{CD}}=\frac{q}{24 \cdot E \cdot I \cdot L} \cdot (L \cdot (x-(a- \frac c2))^4-4 \cdot b \cdot c \cdot x^3+4 \cdot a \cdot b \cdot c \cdot (L+b- \frac{c^2}{4 \cdot a}) \cdot x) \]
\[ \mathrm{Y_{CD}}=\frac{q}{24 \cdot E \cdot I \cdot L} \cdot (L \cdot (x-(a- \frac c2))^4-4 \cdot b \cdot c \cdot x^3+ ... \] \[ ... +4 \cdot a \cdot b \cdot c \cdot (L+b- \frac{c^2}{4 \cdot a}) \cdot x) \]
\[ \mathrm{Y_{DB}}=\frac{q \cdot a \cdot c}{6 \cdot L} \cdot \frac{(L-x)}{E \cdot I} \cdot (-(L-x)^2+b \cdot (L+a- \frac{c^2}{4 \cdot b})) \]
\[ \mathrm{Y_{DB}}=\frac{q \cdot a \cdot c}{6 \cdot L} \cdot \frac{(L-x)}{E \cdot I} \cdot (-(L-x)^2+b \cdot (L+a- \frac{c^2}{4 \cdot b})) \]

FLECHA

Flecha caso 4

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot a \cdot b \cdot c}{6 \cdot E \cdot I \cdot L} \cdot (L+b- \frac{c^2}{4 \cdot a}) \]
\[ \mathrm{\theta_B}=- \frac{q \cdot a \cdot b \cdot c}{6 \cdot E \cdot I \cdot L} \cdot (L+a- \frac{c^2}{4 \cdot b}) \]


CASO 5

Diagrama forma y cargas caso 5

Definición

Viga apoyada-apoyada con una carga repartida aislada que comienza en un apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot a}{L} \cdot (b+ \frac a2) \]
\[ \mathrm{R_B}= \frac{q \cdot a^2}{2 \cdot L} \]
Diagrama de cargas y reacciones caso 5

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{q \cdot a}{L} \cdot (b+ \frac a2)-q \cdot x \]
\[ \mathrm{V_{CB}}=-\frac{q \cdot a^2}{2 \cdot L} \]
Diagrama de Cortantes caso 5

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{q \cdot a}{L} \cdot (b+ \frac a2) \cdot x- \frac {q \cdot x^2}{2} \]
\[ \mathrm{M_{CB}}=\frac{q \cdot a^2}{2 \cdot L} \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\frac{q \cdot a^2}{2} \cdot (1- \frac{a}{2 \cdot L})^2 \]

para:

\[ \mathrm{x_{o}}= a \cdot (1- \frac {a}{2 \cdot L}) \]
Diagrama de momentos caso 5

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{24 \cdot E \cdot I \cdot L} \cdot (L \cdot x^3-4 \cdot a \cdot (b+ \frac a2) \cdot x^2 + a^2 \cdot (L+b)^2) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{24 \cdot E \cdot I \cdot L} \cdot (L \cdot x^3-4 \cdot a \cdot (b+ \frac a2) \cdot x^2 + ... \] \[ ... + a^2 \cdot (L+b)^2) \]
\[ \mathrm{Y_{BC}}=-\frac{q \cdot (L-x) \cdot a^2}{12 \cdot E \cdot I \cdot L} \cdot ((L-x)^2 - L^2 \cdot (1- \frac {a^2}{2 \cdot L^2})) \]
\[ \mathrm{Y_{BC}}=-\frac{q \cdot (L-x) \cdot a^2}{12 \cdot E \cdot I \cdot L} \cdot ((L-x)^2 - L^2 \cdot (1- \frac {a^2}{2 \cdot L^2})) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{216 \cdot E \cdot I\cdot L} \cdot (2 \cdot L^2-a^2) \cdot \sqrt{6 \cdot (2 \cdot L^2-a^2)} \]
\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{216 \cdot E \cdot I\cdot L} \cdot (2 \cdot L^2-a^2) \cdot \sqrt{6 \cdot (2 \cdot L^2-a^2)} \]

para:

\[ a < 0.4531 \cdot L \hspace{2em} x= L-\sqrt{\frac{L^2}{3}-\frac{a^2}{6}} \]
Flecha caso 5

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot a^2}{24 \cdot E \cdot I \cdot L} \cdot (L+b)^2 \]
\[ \mathrm{\theta_B}=- \frac{q \cdot a^2}{12 \cdot E \cdot I} \cdot (1- \frac{a^2}{2 \cdot L^2}) \cdot L \]


CASO 6

Diagrama forma y cargas caso 6

Definición

Viga apoyada-apoyada con una carga uniformemente repartida entre apoyos.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac{q \cdot L}{2} \]
Diagrama de cargas y reacciones caso 6

E. CORTANTES

\[ \mathrm{V_{x}}=q \cdot (\frac L2-x) \]
\[ \mathrm{V_{A}}=-\mathrm{V_{B}}= \frac{q \cdot L}{2} \]
Diagrama de Cortantes caso 6

M. FLECTORES

\[ \mathrm{M_{x}}=\frac{q \cdot x}{2} \cdot (L-x) \]
\[ \mathrm{M_{máx}}=\frac{q \cdot L^2}{8} \hspace{2em} para \hspace{1em} \mathrm{x_{o}}= \frac L2 \]
Diagrama de momentos caso 6

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=\frac{q \cdot x}{24 \cdot E \cdot I} \cdot (x^3- 2 \cdot L \cdot x^2 + L^3) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{5 \cdot q \cdot L^4}{384 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L2 \]
Flecha caso 6

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= -\mathrm{\theta_B}= \frac{q \cdot L^3}{24 \cdot E \cdot I} \]


CASO 7

Diagrama forma y cargas caso 7

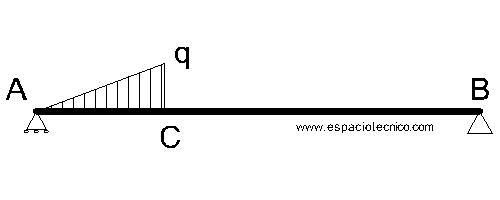
Definición

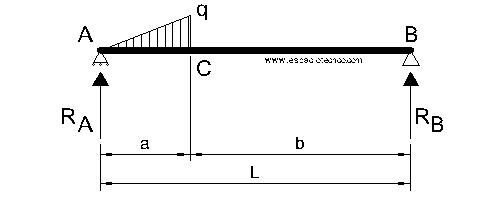
Viga apoyada-apoyada con una carga no uniformemente repartida aislada que comienza en un apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-2 \cdot a) \]
\[ \mathrm{R_B}= \frac{q \cdot a^2}{3 \cdot L} \]
Diagrama de cargas y reacciones caso 7

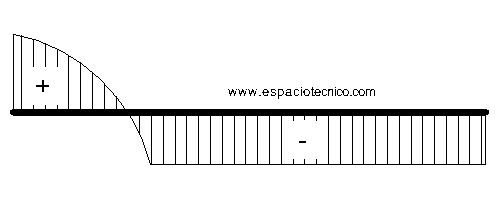
E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-2 \cdot a)- \frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{CB}}=-\frac{q \cdot a^2}{3 \cdot L} \]
Diagrama de Cortantes caso 7

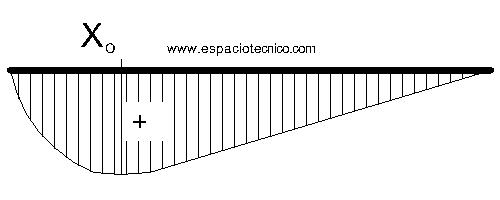
M. FLECTORES

\[ \mathrm{M_{AC}}=q \cdot \frac x6 \cdot ((3- \frac{2 \cdot a}{L}) \cdot a- \frac {x^2}{a}) \]
\[ \mathrm{M_{CB}}=q \cdot \frac{a^2}{3} \cdot (1- \frac xL) \]
\[ \mathrm{M_{máx}}=q \cdot \frac{a^2}{3} \cdot (1- \frac{2 \cdot a}{3 \cdot L}) \cdot \sqrt{1- \frac{2 \cdot a}{3 \cdot L}} \]

para:

\[ \mathrm{x_{o}}=a \cdot \sqrt{1- \frac{2 \cdot a}{3 \cdot L}} \]
Diagrama de momentos caso 7

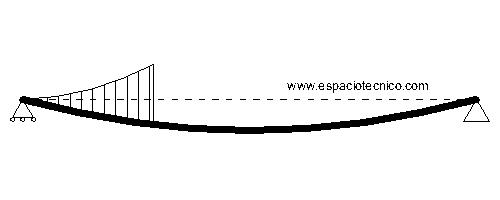
EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot a \cdot E \cdot I \cdot L} \cdot...\] \[... \cdot (3 \cdot L \cdot x^4-10 \cdot (3 \cdot L - 2 \cdot a) \cdot a^2 \cdot x^2 + ... \] \[ ... + a^3 \cdot (40 \cdot L^2-45 \cdot a \cdot L+12 \cdot a^2)) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot a \cdot E \cdot I \cdot L} \cdot...\] \[... \cdot (3 \cdot L \cdot x^4-10 \cdot (3 \cdot L - 2 \cdot a) \cdot a^2 \cdot x^2 + ... \] \[ ... + a^3 \cdot (40 \cdot L^2-45 \cdot a \cdot L+12 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=-\frac{q \cdot a^2}{18 \cdot E \cdot I \cdot L} \cdot (L-x) \cdot ((L-x)^2- L^2 \cdot (1- \frac {3 \cdot a^2}{5 \cdot L^2})) \]
\[ \mathrm{Y_{CB}}=-\frac{q \cdot a^2}{18 \cdot E \cdot I \cdot L} \cdot...\] \[... \cdot (L-x) \cdot ((L-x)^2- L^2 \cdot (1- \frac {3 \cdot a^2}{5 \cdot L^2})) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{9 \cdot E \cdot I\cdot L} \cdot (\frac{L^2}{3}-\frac{a^2}{5}) \cdot \sqrt{\frac{L^2}{3}-\frac{a^2}{5}} \]
\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{9 \cdot E \cdot I\cdot L} \cdot (\frac{L^2}{3}-\frac{a^2}{5}) \cdot \sqrt{\frac{L^2}{3}-\frac{a^2}{5}} \]
Flecha caso 7

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot a^2}{360 \cdot E \cdot I \cdot L} \cdot (40 \cdot L^2-45 \cdot a \cdot L+12 \cdot a^2) \]
\[ \mathrm{\theta_A}= \frac{q \cdot a^2}{360 \cdot E \cdot I \cdot L} \cdot (40 \cdot L^2-45 \cdot a \cdot L+12 \cdot a^2) \]
\[ \mathrm{\theta_B}=- \frac{q \cdot a^2 \cdot L}{18 \cdot E \cdot I} \cdot (1- \frac{3 \cdot a^2}{5 \cdot L^2}) \]


CASO 8

Diagrama forma y cargas caso 8

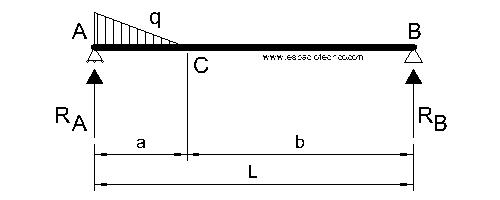
Definición

Viga apoyada-apoyada con una carga no uniformemente repartida aislada que comienza en un apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-a) \]
\[ \mathrm{R_B}= \frac{q \cdot a^2}{6 \cdot L} \]
Diagrama de cargas y reacciones caso 8

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-a)- q \cdot x \cdot (1- \frac{x}{2 \cdot a}) \]
\[ \mathrm{V_{CB}}=-\frac{q \cdot a^2}{6 \cdot L} \]
Diagrama de Cortantes caso 8

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{q \cdot x}{6} \cdot ((3 \cdot a- \frac{a^2}{L})- \frac xa \cdot (3 \cdot a-x)) \]
\[ \mathrm{M_{CB}}=\frac{q \cdot a^2}{6} \cdot (1- \frac xL) \]
\[ \mathrm{M_{máx}}= \frac {q \cdot a^2}{6} \cdot (1- \frac{a}{3 \cdot L})- \frac {q \cdot a^3}{9 \cdot L} \cdot (1- \sqrt{ \frac{a}{3 \cdot L}}) \]
\[ \mathrm{M_{máx}}= \frac {q \cdot a^2}{6} \cdot (1- \frac{a}{3 \cdot L})- \frac {q \cdot a^3}{9 \cdot L} \cdot (1- \sqrt{ \frac{a}{3 \cdot L}}) \]

para:

\[ \mathrm{x_{o}}=a \cdot (1- \sqrt{\frac{a}{3 \cdot L}}) \]
Diagrama de momentos caso 8

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot a \cdot E \cdot I \cdot L} \cdot (3 \cdot L \cdot x^4-15 \cdot a \cdot L \cdot x^3 + ... \] \[ ... + 10 \cdot a^2 \cdot (3 \cdot L-a) \cdot x^2-a^3 \cdot (20 \cdot L^2-15 \cdot a \cdot L+3 \cdot a^2)) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot a \cdot E \cdot I \cdot L} \cdot...\] \[... \cdot (3 \cdot L \cdot x^4-15 \cdot a \cdot L \cdot x^3 + ... \] \[ ... + 10 \cdot a^2 \cdot (3 \cdot L-a) \cdot x^2 + ... \] \[ ... - a^3 \cdot (20 \cdot L^2-15 \cdot a \cdot L+3 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=-\frac{q \cdot a^2 \cdot (L-x)}{360 \cdot E \cdot I \cdot L} \cdot (10 \cdot (L-x)^2- (10 \cdot L^2-3 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=-\frac{q \cdot a^2 \cdot (L-x)}{360 \cdot E \cdot I \cdot L} \cdot (10 \cdot (L-x)^2- (10 \cdot L^2-3 \cdot a^2)) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{18 \cdot E \cdot I\cdot L} \cdot (\frac{L^2}{3}-\frac{a^2}{10}) \cdot \sqrt{\frac{L^2}{3}-\frac{a^2}{10}} \]
\[ \mathrm{Y_{máx}}=\frac{q \cdot a^2}{18 \cdot E \cdot I\cdot L} \cdot (\frac{L^2}{3}-\frac{a^2}{10}) \cdot \sqrt{\frac{L^2}{3}-\frac{a^2}{10}} \]
Flecha caso 8

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot a^2}{360 \cdot E \cdot I \cdot L} \cdot (20 \cdot L^2-15 \cdot a \cdot L+3 \cdot a^2) \]
\[ \mathrm{\theta_A}= \frac{q \cdot a^2}{360 \cdot E \cdot I \cdot L} \cdot (20 \cdot L^2-15 \cdot a \cdot L+3 \cdot a^2) \]
\[ \mathrm{\theta_B}=- \frac{q \cdot a^2 \cdot L}{36 \cdot E \cdot I} \cdot (1- \frac{3 \cdot a^2}{10 \cdot L^2}) \]


CASO 9

Diagrama forma y cargas caso 9

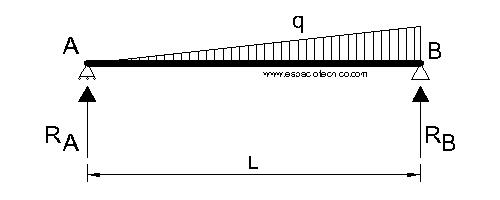
Definición

Viga apoyada-apoyada con una carga no uniformemente repartida de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot L}{6} \]
\[ \mathrm{R_B}= \frac{q \cdot L}{3} \]
Diagrama de cargas y reacciones caso 9

E. CORTANTES

\[ \mathrm{V_{x}}=\frac{q \cdot L}{6} \cdot (1-3 \cdot \frac{x^2}{L^2}) \]
Diagrama de Cortantes caso 9

M. FLECTORES

\[ \mathrm{M_{x}}=\frac{q \cdot L}{6} \cdot x \cdot (1- \frac{x^2}{L^2}) \]
\[ \mathrm{M_{máx}}= \frac {q \cdot L^2}{9 \cdot \sqrt{3}} \hspace{2em} para \hspace{1em} \mathrm{x_{o}}=\frac{L}{\sqrt{3}} \]
Diagrama de momentos caso 9

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=\frac{q \cdot L^3 \cdot x}{360 \cdot E \cdot I} \cdot (7-10 \cdot \frac{x^2}{L^2}+3 \cdot \frac{x^4}{L^4}) \]
\[ \mathrm{Y_{x}}=\frac{q \cdot L^3 \cdot x}{360 \cdot E \cdot I} \cdot (7-10 \cdot \frac{x^2}{L^2}+3 \cdot \frac{x^4}{L^4}) \]

FLECHA

\[ \mathrm{Y_{máx}}=0,00652 \cdot \frac{q \cdot L^4}{E \cdot I} \hspace{2em} para \hspace{1em} x=0,5193 \cdot L \]
\[ \mathrm{Y_{máx}}=0,00652 \cdot \frac{q \cdot L^4}{E \cdot I} \hspace{2em} para \hspace{1em} x=0,5193 \cdot L \]
Flecha caso 9

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{7}{360} \cdot \frac{q \cdot L^3}{E \cdot I} \]
\[ \mathrm{\theta_B}=- \frac{1}{45} \cdot \frac{q \cdot L^3}{E \cdot I} \]


CASO 10

Diagrama forma y cargas caso 10

Definición

Viga apoyada-apoyada con dos cargas simetricas no uniformemente repartidas de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot L}{4} \]
\[ \mathrm{R_B}= \frac{q \cdot L}{4} \]
Diagrama de cargas y reacciones caso 10

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{q \cdot L}{4}-q \cdot (1- \frac{x}{L}) \cdot x \]
\[ \mathrm{V_{CB}}=-\frac{q \cdot L}{4}+q \cdot (1- \frac{x}{L}) \cdot x \]
Diagrama de Cortantes caso 10

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{q \cdot L}{4} \cdot x-q \cdot x^2 \cdot (\frac 12 - \frac{x}{3 \cdot L}) \]
\[ \mathrm{M_{CB}}=\frac{q \cdot L}{12} \cdot (L-3 \cdot x)+q \cdot x^2 \cdot (\frac 12 - \frac{x}{3 \cdot L}) \]
\[ \mathrm{M_{CB}}=\frac{q \cdot L}{12} \cdot (L-3 \cdot x)+q \cdot x^2 \cdot (\frac 12 - \frac{x}{3 \cdot L}) \]
\[ \mathrm{M_{máx}}= \frac{1}{24} \cdot q \cdot L^2 \hspace{2em} para \hspace{1em} \mathrm{x_{o}}=\frac L2 \]
Diagrama de momentos caso 10

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=-\frac{q \cdot x}{192 \cdot E \cdot I \cdot L} \cdot (\frac{16}{5} \cdot x^4-8 \cdot L \cdot x^3+8 \cdot L^2 \cdot x^2-3 \cdot L^4) \]
\[ \mathrm{Y_{AC}}=-\frac{q \cdot x}{192 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (\frac{16}{5} \cdot x^4-8 \cdot L \cdot x^3+8 \cdot L^2 \cdot x^2-3 \cdot L^4) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{3 \cdot q \cdot L^4}{640 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L2 \]
\[ \mathrm{Y_{máx}}=\frac{3 \cdot q \cdot L^4}{640 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L2 \]
Flecha caso 10

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot L^3}{64 \cdot E \cdot I} \]
\[ \mathrm{\theta_B}=- \frac{q \cdot L^3}{64 \cdot E \cdot I} \]


CASO 11

Diagrama forma y cargas caso 11

Definición

Viga apoyada-apoyada con una carga repartida triangular no simétrica de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac q6 \cdot (L+b) \]
\[ \mathrm{R_B}= \frac q6 \cdot (L+a) \]
Diagrama de cargas y reacciones caso 11

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac q6 \cdot (L+b)-\frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{CB}}=-\frac q6 \cdot (L+a)+\frac{q \cdot (L-x)^2}{2 \cdot b} \]
Diagrama de Cortantes caso 11

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac q6 \cdot (2 \cdot L-a) \cdot x-\frac{q \cdot x^3}{6 \cdot a} \]
\[ \mathrm{M_{CB}}=\frac q6 \cdot (L+a) \cdot (L-x)-\frac q6 \cdot \frac{q \cdot (L-x)^3}{L-a} \]
\[ \mathrm{M_{CB}}=\frac q6 \cdot (L+a) \cdot (L-x)-\frac q6 \cdot \frac{q \cdot (L-x)^3}{L-a} \]
\[ \mathrm{M_{máx}}=\frac q9 \cdot \sqrt{\frac a3 \cdot (2 \cdot L-a)^3} \hspace{1em} para \hspace{1em} a > b \]
\[ \mathrm{x_{o}}= \sqrt{\frac a3 \cdot (2 \cdot L-a)} \]
Diagrama de momentos caso 11

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot E \cdot I} \cdot (\frac 3a \cdot x^4-10 \cdot (L+b) \cdot x^2+(L+b) \cdot (7 \cdot L^2-3 \cdot b^2)) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{360 \cdot E \cdot I} \cdot ... \] \[ ... \cdot (\frac 3a \cdot x^4-10 \cdot (L+b) \cdot x^2+(L+b) \cdot (7 \cdot L^2-3 \cdot b^2)) \]
\[ \mathrm{Y_{CB}}=\frac{q \cdot (L-x)}{360 \cdot E \cdot I} \cdot (\frac 3b \cdot (L-x)^4-10 \cdot (L+a) \cdot (L-x)^2+(L+a) \cdot (7 \cdot L^2-3 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=\frac{q \cdot (L-x)}{360 \cdot E \cdot I} \cdot ... \] \[ ... \cdot (\frac 3b \cdot (L-x)^4-10 \cdot (L+a) \cdot (L-x)^2 + ... \] \[ ... + (L+a) \cdot (7 \cdot L^2-3 \cdot a^2)) \]

FLECHA

Flecha caso 11

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{q \cdot (L+b)}{360 \cdot E \cdot I} \cdot (7 \cdot L^2-3 \cdot b^2) \]
\[ \mathrm{\theta_B}=- \frac{q \cdot (L+a)}{360 \cdot E \cdot I} \cdot (7 \cdot L^2-3 \cdot a^2) \]


CASO 12

Diagrama forma y cargas caso 12

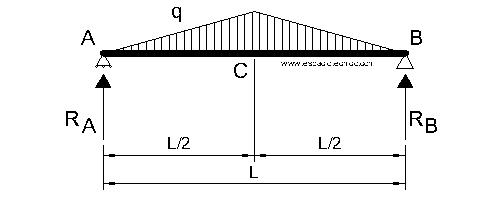
Definición

Viga apoyada-apoyada con una carga repartida triangular simétrica de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac {q \cdot L}{4} \]
\[ \mathrm{R_B}= \frac {q \cdot L}{4} \]
Diagrama de cargas y reacciones caso 12

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac {q \cdot L}{4}-\frac{q \cdot x^2}{L} \]
\[ \mathrm{V_{CB}}=\frac {q \cdot L}{4}+q \cdot \frac{(L-x)^2}{L} \]
Diagrama de Cortantes caso 12

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac {q \cdot L}{4} \cdot (x-\frac{4 \cdot x^3}{3 \cdot L^2}) \]
\[ \mathrm{M_{CB}}=\frac {q \cdot L}{4} \cdot (-\frac L3 +3 \cdot x - \frac{4 \cdot x^2}{L}+\frac{4 \cdot x^3}{3 \cdot L^2}) \]
\[ \mathrm{M_{CB}}=\frac {q \cdot L}{4} \cdot (-\frac L3 +3 \cdot x - \frac{4 \cdot x^2}{L}+\frac{4 \cdot x^3}{3 \cdot L^2}) \]
\[ \mathrm{M_{máx}}=\frac {q \cdot L^2}{12} \hspace{2em} para \hspace{1em} \mathrm{x_{o}}= \frac L2 \]
Diagrama de momentos caso 12

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot L^3 \cdot x}{960 \cdot E \cdot I} \cdot (25-40 \cdot \frac{x^2}{L^2}+16 \cdot \frac{x^4}{L^4} ) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot L^3 \cdot x}{960 \cdot E \cdot I} \cdot (25-40 \cdot \frac{x^2}{L^2}+16 \cdot \frac{x^4}{L^4} ) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{q \cdot L^4}{120 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L2 \]
\[ \mathrm{Y_{máx}}=\frac{q \cdot L^4}{120 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L2 \]
Flecha caso 12

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= -\mathrm{\theta_B}=\frac{5 \cdot q \cdot L^3}{192 \cdot E \cdot I} \]


CASO 13

Diagrama forma y cargas caso 13

Definición

Viga apoyada-apoyada con una carga repartida trapezoidal de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \frac L6 \cdot (2 \cdot \mathrm{q_1}+\mathrm{q_2}) \]
\[ \mathrm{R_B}= \frac L6 \cdot (\mathrm{q_1}+2 \cdot \mathrm{q_2}) \]
Diagrama de cargas y reacciones caso 13

E. CORTANTES

\[ \mathrm{V_{x}}=\frac {(2 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^2-6 \cdot L \cdot \mathrm{q_1} \cdot x+3 \cdot (\mathrm{q_1}-\mathrm{q_2}) \cdot x^2}{L \cdot 6} \]
\[ \mathrm{V_{x}}=\frac {(2 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^2-6 \cdot L \cdot \mathrm{q_1} \cdot x+3 \cdot (\mathrm{q_1}-\mathrm{q_2}) \cdot x^2}{L \cdot 6} \]
Diagrama de Cortantes caso 13

M. FLECTORES

\[ \mathrm{M_{x}}=\frac {(2 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^2 \cdot x-3 \cdot L \cdot \mathrm{q_1} \cdot x^2+(\mathrm{q_1}-\mathrm{q_2}) \cdot x^3}{6 \cdot L} \]
\[ \mathrm{M_{x}}=\frac {(2 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^2 \cdot x-3 \cdot L \cdot \mathrm{q_1} \cdot x^2+(\mathrm{q_1}-\mathrm{q_2}) \cdot x^3}{6 \cdot L} \]
\[ \mathrm{M_{máx}}= Esta \hspace{0.6em} comprendido \hspace{0.6em} entre \hspace{0.6em} 0,125 \cdot \frac {L^2}{2} \cdot (\mathrm{q_1}+\mathrm{q_2}) \hspace{0.6em} y \hspace{0.6em} ...\] \[... \hspace{0.6em} y \hspace{0.6em} 0,128 \cdot \frac {L^2}{2} \cdot (\mathrm{q_1}+\mathrm{q_2}) \]
\[ \mathrm{M_{máx}}= Esta \hspace{0.6em} comprendido \hspace{0.6em} entre \] \[ 0,125 \cdot \frac {L^2}{2} \cdot (\mathrm{q_1}+\mathrm{q_2}) \hspace{0.6em} \] \[ y \] \[ 0,128 \cdot \frac {L^2}{2} \cdot (\mathrm{q_1}+\mathrm{q_2}) \]

para:

\[ \mathrm{X_{o}}=\frac {L}{\mathrm{q_2}-\mathrm{q_1}} \cdot (-\mathrm{q_1}+\sqrt{\frac 13 \cdot (\mathrm{q_1}^2+\mathrm{q_2}^2+\mathrm{q_1} \cdot \mathrm{q_2})}) \]
\[ \mathrm{X_{o}}=\frac {L}{\mathrm{q_2}-\mathrm{q_1}} \cdot (-\mathrm{q_1}+\sqrt{\frac 13 \cdot (\mathrm{q_1}^2+\mathrm{q_2}^2+\mathrm{q_1} \cdot \mathrm{q_2})}) \]
Diagrama de momentos caso 13

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=\frac{x \cdot (L-x)}{360 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (3 \cdot (\mathrm{q_1}-\mathrm{q_2}) \cdot x^3-3 \cdot (4 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L \cdot x^2 + ... \] \[ ... + (8 \cdot \mathrm{q_1}+7 \cdot \mathrm{q_2}) \cdot L^2 \cdot x+(8 \cdot \mathrm{q_1}+7 \cdot \mathrm{q_2}) \cdot L^3) \]
\[ \mathrm{Y_{x}}=\frac{x \cdot (L-x)}{360 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (3 \cdot (\mathrm{q_1}-\mathrm{q_2}) \cdot x^3-3 \cdot (4 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L \cdot x^2 + ... \] \[ ... + (8 \cdot \mathrm{q_1}+7 \cdot \mathrm{q_2}) \cdot L^2 \cdot x+(8 \cdot \mathrm{q_1}+7 \cdot \mathrm{q_2}) \cdot L^3) \]

FLECHA

\[ Esta \hspace{0.6em} comprendida \hspace{0.6em} entre \hspace{0.6em} 0,01302 \cdot \frac{(\mathrm{q_1}+ \mathrm{q_2}) \cdot L^4}{2 \cdot E \cdot I} \hspace{0.6em} y \hspace{0.6em} ... \] \[ ... \hspace{0.6em} y \hspace{0.6em} 0,01304 \cdot \frac{(\mathrm{q_1}+ \mathrm{q_2}) \cdot L^4}{2 \cdot E \cdot I} \]
\[ Esta \hspace{0.6em} comprendida \hspace{0.6em} entre \hspace{0.6em} 0,01302 \cdot \frac{(\mathrm{q_1}+ \mathrm{q_2}) \cdot L^4}{2 \cdot E \cdot I} \hspace{0.6em} y \hspace{0.6em} ... \] \[ ... \hspace{0.6em} y \hspace{0.6em} 0,01304 \cdot \frac{(\mathrm{q_1}+ \mathrm{q_2}) \cdot L^4}{2 \cdot E \cdot I} \]
Flecha caso 13

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{L^3}{360 \cdot E \cdot I}\cdot (8 \cdot \mathrm{q_1}+7 \cdot \mathrm{q_2}) \]
\[ \mathrm{\theta_B}=-\frac{L^3}{360 \cdot E \cdot I}\cdot (7 \cdot \mathrm{q_1}+8 \cdot \mathrm{q_2}) \]


CASO 14

Diagrama forma y cargas caso 14

Definición

Viga apoyada-apoyada con una carga repartida trapezoidal simetrica de apoyo a apoyo.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac q2 \cdot (L-a) \]
Diagrama de cargas y reacciones caso 14

E. CORTANTES

\[ \mathrm{V_{AC}}= \frac q2 \cdot (L-a)-q \frac {x^2}{2 \cdot a} \]
\[ \mathrm{V_{CD}}= \frac q2 \cdot (L-2 \cdot x) \]
\[ \mathrm{V_{DB}}= -\frac q2 \cdot (L-a) + \frac q2 \cdot \frac {(L-x)^2}{a} \]
Diagrama de Cortantes caso 14

M. FLECTORES

\[ \mathrm{M_{AC}}= \frac q2 \cdot (L-a) \cdot x- \frac q6 \cdot \frac{x^3}{a} \]
\[ \mathrm{M_{CD}}= \frac q6 \cdot (3 \cdot L \cdot x-a^2-3 \cdot x^2) \]
\[ \mathrm{M_{DB}}= \frac q2 \cdot (L-a) \cdot (L-x) - \frac {q}{6 \cdot a} \cdot ( L-x)^3 \]
\[ \mathrm{M_{DB}}= \frac q2 \cdot (L-a) \cdot (L-x) - \frac {q}{6 \cdot a} \cdot ( L-x)^3 \]
\[ \mathrm{M_{máx}}= \frac{q}{24} \cdot (3 \cdot L^2-4 \cdot a^2) \hspace{2em} para \hspace{1em} \mathrm{x_{o}}= \frac L2 \]
\[ \mathrm{M_{máx}}= \frac{q}{24} \cdot (3 \cdot L^2-4 \cdot a^2) \hspace{2em} para \hspace{1em} \mathrm{x_{o}}= \frac L2 \]
Diagrama de momentos caso 14

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{E \cdot I} \cdot ... \] \[ ... \cdot (\frac{x^4}{120 \cdot a} - \frac{(L-a)}{12} \cdot x^2 + \frac{L^2 \cdot (L+b)}{192} \cdot (5- \frac{b^2}{L^2})) \]
\[ \mathrm{Y_{AC}}=\frac{q \cdot x}{E \cdot I} \cdot ... \] \[ ... \cdot (\frac{x^4}{120 \cdot a} - \frac{(L-a)}{12} \cdot x^2 + \frac{L^2 \cdot (L+b)}{192} \cdot (5- \frac{b^2}{L^2})) \]
\[ \mathrm{Y_{CD}}=\frac{q}{E \cdot I} \cdot ... \] \[ ... \cdot (\frac{x^4}{24} - \frac{(L \cdot x^3)}{12} + \frac{a^2 \cdot x^2}{12} + \frac{L}{24} \cdot (L^2-2 \cdot a^2) \cdot x + \frac{a^4}{120}) \]
\[ \mathrm{Y_{CD}}=\frac{q}{E \cdot I} \cdot ... \] \[ ... \cdot (\frac{x^4}{24} - \frac{(L \cdot x^3)}{12} + \frac{a^2 \cdot x^2}{12} + \frac{L}{24} \cdot (L^2-2 \cdot a^2) \cdot x + \frac{a^4}{120}) \]

FLECHA

\[ \mathrm{Y_{máx}}= \frac{q}{1920 \cdot E \cdot I} \cdot (5 \cdot L^2-4 \cdot a^2)^2 \hspace{2em} para \hspace{1em} x= \frac L2 \]
\[ \mathrm{Y_{máx}}= \frac{q}{1920 \cdot E \cdot I} \cdot (5 \cdot L^2-4 \cdot a^2)^2 \hspace{2em} para \hspace{1em} x= \frac L2 \]
Flecha caso 14

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=- \mathrm{\theta_B}= \frac{q \cdot L^2}{192 \cdot E \cdot I} \cdot (L+b) \cdot (5- \frac{b^2}{L^2}) \]


CASO 15

Diagrama forma y cargas caso 15

Definición

Viga apoyada-apoyada con un momento en un apoyo.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac ML \]
Diagrama de cargas y reacciones caso 15

E. CORTANTES

\[ \mathrm{V_{x}}= \frac ML \]
Diagrama de Cortantes caso 15

M. FLECTORES

\[ \mathrm{M_{x}}= -M \cdot (1- \frac xL) \]
Diagrama de momentos caso 15

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=-\frac{M \cdot L}{6 \cdot E \cdot I} \cdot (L-x)\cdot (1-(\frac{L-x}{L})^2) \]
\[ \mathrm{Y_{x}}=-\frac{M \cdot L}{6 \cdot E \cdot I} \cdot (L-x)\cdot (1-(\frac{L-x}{L})^2) \]

FLECHA

\[ \mathrm{Y_{máx}}= -\frac{M \cdot L^2}{9 \cdot \sqrt{3} \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= L \cdot (1- \frac {1}{\sqrt{3}}) \]
\[ \mathrm{Y_{máx}}= -\frac{M \cdot L^2}{9 \cdot \sqrt{3} \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= L \cdot (1- \frac {1}{\sqrt{3}}) \]
Flecha caso 15

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=- \frac{M \cdot L}{3 \cdot E \cdot I} \]
\[ \mathrm{\theta_B}= \frac{M \cdot L}{6 \cdot E \cdot I} \]


CASO 16

Diagrama forma y cargas caso 16

Definición

Viga apoyada-apoyada con dos momentos, uno en cada apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac {\mathrm{M_a}-\mathrm{M_b}}{L} \] \[ * \hspace{0.3em} Los \hspace{0.6em} sentidos \hspace{0.6em} serán \hspace{0.6em} contrarios \hspace{0.6em} si \] \[ |\mathrm{M_b}| > |\mathrm{M_a}| \]
Diagrama de cargas y reacciones caso 16

E. CORTANTES

\[ \mathrm{V_{x}}= \frac{\mathrm{M_a}-\mathrm{M_b}}{L} \]
Diagrama de Cortantes caso 16

M. FLECTORES

\[ \mathrm{M_{x}}= - \frac{\mathrm{M_a}}{L} \cdot (L-x )- \frac{\mathrm{M_b}}{L} \cdot x \]
Diagrama de momentos caso 16

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=-\frac{\mathrm{M_a} \cdot x}{6 \cdot E \cdot I} \cdot (L-x)\cdot (1+(\frac{(L-x)}{L}+ \frac{\mathrm{M_b}}{\mathrm{M_a}} \cdot (1+ \frac xL)) \]
\[ \mathrm{Y_{x}}=-\frac{\mathrm{M_a} \cdot x}{6 \cdot E \cdot I} \cdot (L-x)\cdot (1+(\frac{(L-x)}{L}+ \frac{\mathrm{M_b}}{\mathrm{M_a}} \cdot (1+ \frac xL)) \]

FLECHA

Flecha caso 16

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=- \frac{L}{6 \cdot E \cdot I} \cdot (2 \cdot \mathrm{M_a} + \mathrm{M_b}) \]
\[ \mathrm{\theta_B}= \frac{L}{6 \cdot E \cdot I} \cdot (\mathrm{M_a} + 2 \cdot \mathrm{M_b}) \]


CASO 17

Diagrama forma y cargas caso 17

Definición

Viga apoyada-apoyada con dos momentos, uno en cada apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac {\mathrm{M_a}+\mathrm{M_b}}{L} \]
Diagrama de cargas y reacciones caso 17

E. CORTANTES

\[ \mathrm{V_{x}}= \frac{\mathrm{M_a}+\mathrm{M_b}}{L} \]
Diagrama de Cortantes caso 17

M. FLECTORES

\[ \mathrm{M_{x}}= \frac 1L \cdot (\mathrm{M_a} + \mathrm{M_b}) \cdot x - \mathrm{M_a} \]
Diagrama de momentos caso 17

EC. ELÁSTICA

\[ \mathrm{Y_{x}}=\frac{x \cdot (L^2 - x^2)}{6 \cdot E \cdot I \cdot L} \cdot (\mathrm{M_b} - \mathrm{M_a} \cdot (L+x) \cdot L) \]
\[ \mathrm{Y_{x}}=\frac{x \cdot (L^2 - x^2)}{6 \cdot E \cdot I \cdot L} \cdot (\mathrm{M_b} - \mathrm{M_a} \cdot (L+x) \cdot L) \]

FLECHA

Flecha caso 17

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=- \frac{L}{6 \cdot E \cdot I} \cdot (2 \cdot \mathrm{M_a} - \mathrm{M_b}) \]
\[ \mathrm{\theta_B}=- \frac{L}{6 \cdot E \cdot I} \cdot (2 \cdot \mathrm{M_b} - \mathrm{M_a}) \]


CASO 18

Diagrama forma y cargas caso 18

Definición

Viga apoyada-apoyada con un momento aislado.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac ML \]
Diagrama de cargas y reacciones caso 18

E. CORTANTES

\[ \mathrm{V_{x}}= -\frac ML \]
Diagrama de Cortantes caso 18

M. FLECTORES

\[ \mathrm{M_{AC}}= - \frac ML \cdot x \]
\[ \mathrm{M_{CB}}= \frac ML \cdot (L-x) \]
\[ \mathrm{M_{C}}^{izq}= -\frac ML \cdot a \hspace{3em} \mathrm{M_{C}}^{der}= \frac ML \cdot b \] \[ |M|=|\mathrm{M_{C}}^{izq}| + |\mathrm{M_{C}}^{der}| \]
Diagrama de momentos caso 18

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{M \cdot x}{6 \cdot E \cdot I \cdot L} \cdot (x^2 + 3 \cdot b^2- L^2) \]
\[ \mathrm{Y_{AC}}=\frac{M \cdot x}{6 \cdot E \cdot I \cdot L} \cdot (x^2 + 3 \cdot b^2- L^2) \]
\[ \mathrm{Y_{BC}}=\frac{M \cdot (L-x)}{6 \cdot E \cdot I \cdot L} \cdot (-x^2 + 2 \cdot L \cdot x - 3 \cdot a^2) \]
\[ \mathrm{Y_{BC}}=\frac{M \cdot (L-x)}{6 \cdot E \cdot I \cdot L} \cdot (-x^2 + 2 \cdot L \cdot x - 3 \cdot a^2) \]

FLECHA

\[ \mathrm{Y_{C}}= \frac{M \cdot a \cdot b}{3 \cdot E \cdot I \cdot L} \cdot (b-a) \]
Flecha caso 18

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac{M}{6 \cdot E \cdot I \cdot L} \cdot (3 \cdot b^2 - L^2) \]
\[ \mathrm{\theta_B}= \frac{M}{6 \cdot E \cdot I \cdot L} \cdot (3 \cdot a^2 - L^2) \]
\[ \mathrm{\theta_C}= \frac{M}{3 \cdot E \cdot I \cdot L^2} \cdot (a^3 + b^3) \]